Viscous fingering phenomenon

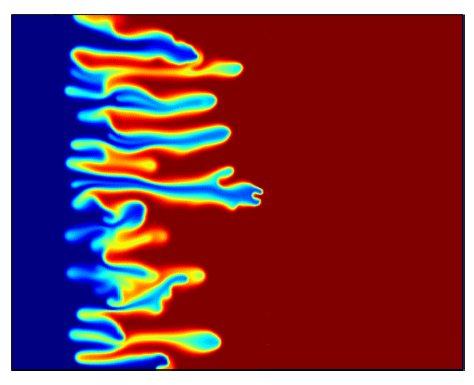
Viscous fingering phenomenon is the instability that occur when you inject a less viscous liquid into a more viscous liquid. If the experiment is done in a thin layer between two glasses, then it is called the Hele-Shaw cell. We consider the displacement of miscible and immiscible fluids in a porous medium. For the one-phase miscible displacement the governing equations are written as follows (the Peaceman model): $$ c_t + \mathrm{div}(u\cdot c)=\varepsilon \Delta c, $$ $$ u=-\frac{k}{\mu(c)}\nabla p, $$ $$ \mathrm{div}(u)=0. $$ Here the unknown functions are:

• $c=c(x,y,t)\in[0,1]$ — concentration of the more viscous fluid inside a less viscous fluid;
• $u=u(x,y,t)$ — velocity of fluid;
• $p=p(x,y,t)$ — pressure.

The function $\mu(c)$ is the viscosity function and it’s inverse $m(c)=1/\mu(c)$ is the mobility function. Imagine that the initial condition is a slightly perturbed Heavy-side function: $$ c(x,y,0) = \mathbb{1}_{x>0} + \eta, \quad \eta\text{ is a small perturbation} $$ Then the instabilities (as in the picture above) will appear and we are interested in the asymptotic behavior of the solution $c$ as $t\to\infty$.

The experimental and numerical analysis shows the linear growth of the most ‘‘fastest’’ finger and the ‘‘slowest’’ finger. So our aim is to find velocities $v_f$ and $v_b$ (f from front, b from back) such that for all $v>v^f$ $$ \lim\limits_{t\to\infty}\sup\limits_{x>v t} c(x,y,t)=1, $$ and for all $v<v^b$ $$ \lim\limits_{t\to\infty}\inf\limits_{x<v t} c(x,y,t)=0. $$ Such kind of result is proved by Felix Otto (2006) for the Peaceman model under the assumption of transeverse flow equilibrium condition (TFE model): $$ c_t + \mathrm{div}(u\cdot c)=\varepsilon \Delta c, $$ $$ u=(u^1, u^2), u^1=\frac{m(c)}{\overline{m(c)}}, $$ $$ \mathrm{div}(u)=0, $$ Here $\overline{m(c)}$ is the average in $y$-direction (for fixed $x$) of the function $m(c(x,y,t))$. Our research is aimed at numerical investigating the linear growth of the considered models, and possible theoretical theatment of the model.