Small ball probabilities for Gaussian processes

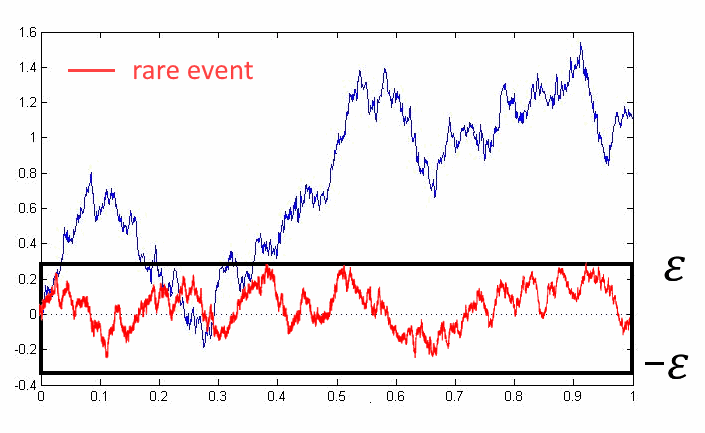
Given a Gaussian process $X(t)$, $t\in[0,1]$, with zero mean, we are interested in the asymptotic behavior of the probability $$ \mathbb{P}(||X(t)||<\varepsilon), \quad \text{as }\varepsilon\to0, $$ which is called small ball probabilities (or small deviation probabilities). Here $||X(t)||$ is some norm.

For example, for $|| X(t)||=\sup\limits_{t\in[0,1]}|X(t)|$ this value is just a probability that the trajectory of the process $X(t)$ stays in a small $\varepsilon$-neighbourhood near it’s mean value for all times (see figure above), which is usually a *rare event*. For example, for a Brownian motion

$$ \mathbb{P}(||X(t)||<\varepsilon)\sim C\cdot\varepsilon\cdot \exp\left(-\frac18\varepsilon^{-2}\right), \quad \text{as }\varepsilon\to0, $$ the probability is exponentially small. The main question of my interest is the following: imagine you have two processes $X_0(t)$ and it’s finite dimensional perturbation $X(t)$. How their small ball probabilities are related to each other? You can prove some general theorems, but many inetersting examples (i.e. coming from statistics) are not obeying the assumptions and need individual analysis. My research on the topic is the publications below.