Conservation laws

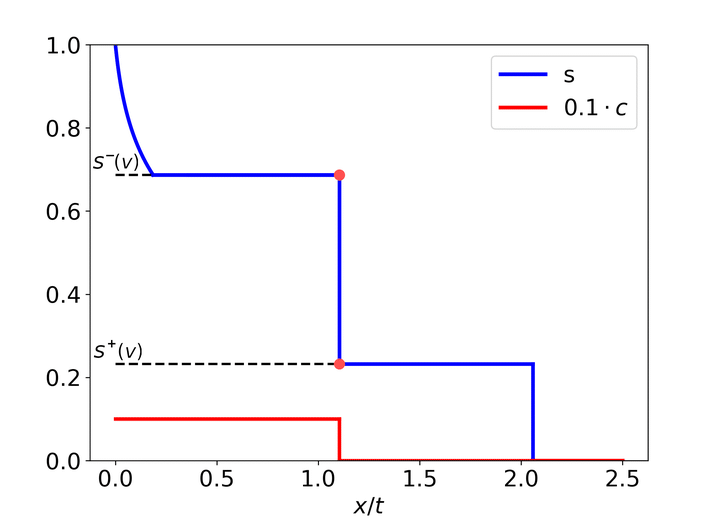
We study the existence, uniqueness and stability of solutions to some systems of conservation laws. Right now we are working on the non-uniqueness of vanishing viscosity admissible solutions for a Riemann problem for the system of conservation laws ($x\in\mathbb{R}$, $t>0$): $$ s_t + f(s, c)_x = 0, $$ $$ (cs + a(c))_t + (cf(s,c))_x = 0, $$ with initial data $s(x,0)=c(x,0)=1$ for $x<0$ and $s(x,0)=s(x,0)=0$ for $x>0$. Here

• $s=s(x,t)\in[0,1]$ is the water phase saturation
• $c=c(x,t)\in[0,1]$ is the concentration of the chemical agent in the water phase
• function $f(s,c)$ denotes the fractional flow of water (the Buckley–Leverett function)
• function $a(c)$ denotes the chemical’s adsorption on the rock

It is commonly assumed that $f$ is an S-shaped function of $s$ for every $c$, and $a$ is an increasing concave function.

Our aim is to prove that when the flow function depends non-monotonically on the concentration of chemicals, non classical shocks appear (undercompressive shocks/transitional waves), which depend on the ratio of dissipative coefficients, and cause non-uniqueness of solutions. Similar observation was made in a recent work by W. Shen (2017) and in a paper by Entov & Kerimov (1986) for different models of dissipation terms.

After the solution is found (and is unique), the next natural question is the stability of the solution under linear, nonlinear perturbations, and asymptotic stability as $t\to\infty$.